Analysis of Common Base Amplifier (CB) using h-parameter

Engineeering Projects

Analysis of Common Base Amplifier (CB) using h-parameter:

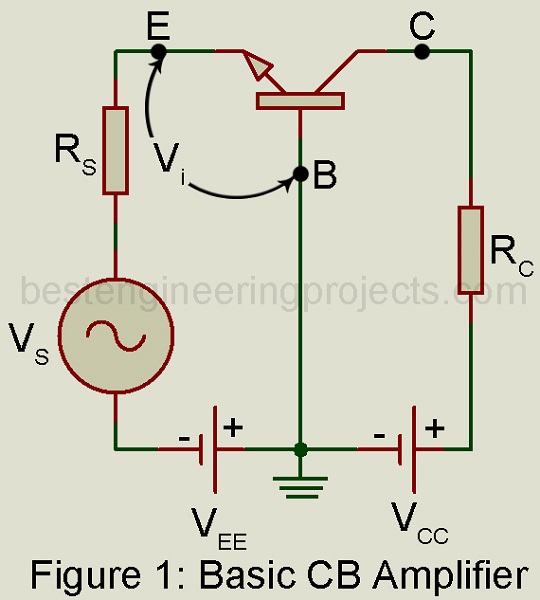
Figure 1 gives the basic circuit of a transistor (NPN type) used as a common base (CB) amplifier. In this case, Vs is the signal voltage, Vi is the actual voltage at the input terminals and V0 is the output voltage.

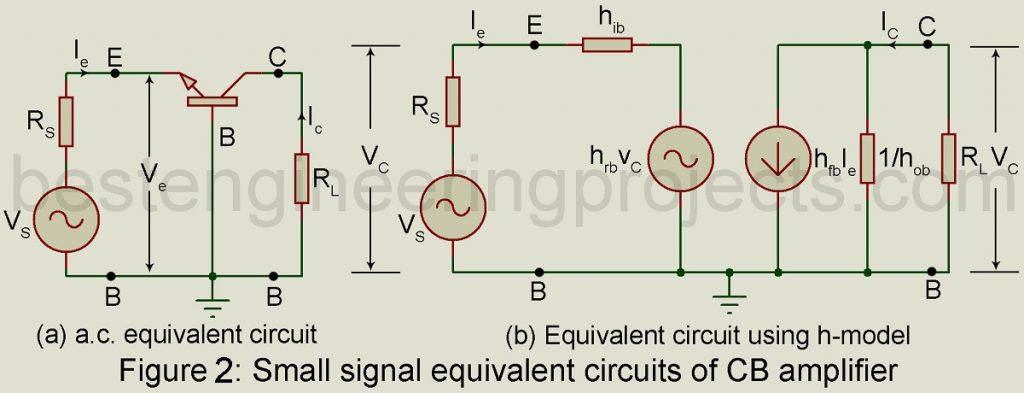
Figure 2(a) gives the a.c. equivalent circuit obtained on having removed the dc source. On replacing the CB transistor with its small-signal two generator h-parameter model we get the equivalent circuit of figure 1(b). Here also we assume sinusoidal input. Hence in the equivalent circuit of figure 2(b), we have used RMS valued of voltages and currents namely Ie, Ve, Ic, and Vc.

The equivalent circuit of figure 3 is similar to that of the CE amplifier as shown in the previous article Analysis of common emitter amplifier using h-parameter.

ce amplifier circuit

Hence analysis procedure is exactly the same. The expression of AI, Ri, AV, AIS, AVS and Yo are therefore, the same as for CE amplifier except that h-parameter for CB configuration are used. Thus we get::

Current gain A_I = -\dfrac{I_c}{I_e} = -\dfrac{h_{fb}}{1+h_{ob}\times R_L}        …..(1)

Input resistance R_i = \dfrac{V_e}{I_e} = h_{ib} -\dfrac{h_{fb}\times h_{rb}}{h_{ob} + Y_L}         ……(2)

Where Y_L = \dfrac{1}{R_L}

small signal circuits of CB amplifier

Voltage Gain A_V = \dfrac{V_c}{V_e} = \dfrac{A_I \times R_L}{R_i}     …..(3)

Output admittance Y_0 = \dfrac{I_c}{V_c} = h_{ob} -\dfrac{h_{fb} \times h_{rb}}{h_{ib} + R_s}        …..(4)

Overall voltage gain A_{VS} = \dfrac{V_c}{V_s} = A_V \times \dfrac{R_i}{R_i + R_s}       …..(5)

Overall current gain A_{IS} = \dfrac{I_L}{I_s} = A_I \dfrac{R_s}{R_i + R_s}        …..(6)

Power Gain A_P = \dfrac{P_L}{P_i} = A_V \times A_I = A_{I2} \times \dfrac{R_L}{R_i}         ……(7)

Equations (1) and (7) may be used to calculate current gain etc. in terms of CB h-parameter by corresponding CE h-parameters.

Example 1: A transistor in CB configuration is driven by a voltage source Vs of internal resistance Rs = 1000. The load impedance is a resistor RL = 4k. the h-parameters are : hib = 220, hrb = 3 \times 10^{-4}, hfb = – 0.98 and h0b = 0.5 \mu S. For this amplifier, calculate the current gain AI, input resistance Ri, voltage gain AV, overall voltage gain AVS, overall current gain AIS output resistance R0 and power gain Ap.

Solution:

Current gain A_I = -\dfrac{h_{fb}}{1 + h_{ob}\times R_L} = \dfrac{-(-0.98)}{1 + (0.5 \times 10^{-6} \times 4000)} = 0.98

Input impedance R_i = h_{ib} + h_{rb} \times A_I \times R_L = 22 + (3 \times 10^{-4})(0.98)(4000) = 23.18

Voltage gain A_V = \dfrac{R_I R_L}{R_i} = \dfrac{0.98 \times 4000}{23.18} = 169

Overall voltage gain A_{VS} = \dfrac{A_V R_i}{R_i + R_s} = \dfrac{169 \times 23.18}{23.18 + 1000} = 3.8

Overall current gain A_{IS} = \dfrac{A_I R_s}{R_i + R_s} = \dfrac{0.98 \times 1000}{23.18 + 1000} = 0.958

Output admittance Y_0 = h_{ob} -\dfrac{h_{fb}\times h_{rb}}{h_{ib} + R_s} = (0.5 \times 10^{-6}) -\dfrac{(0.98)(3\times 10^{-4})}{22 + 1000} = 0.78 \times 10^{-6}S

Hence Z_0 = \dfrac{1}{Y_0} = \dfrac{106}{0.78} = 1.282 M

Power gain A_P = A_V \times A_I = 169 \times 0.98 = 166

Leave a Comment